Introduction to Cryptography - Worksheet
In this lesson you will:
- Meet Alice, Bob and Eve;
- See an overview of the process of exchanging secret keys in public;
- See a simple and more complex cipher algorithm working together;
- See how visual cryptography works.
- Learn and discuss some key words and concepts:
- cyptography,
- encryption,
- decryption;
- public-keys and key exchange;
- ciphers: substitution ciphers
- digital signatures
What is cryptography? (5 minutes)
Crypto- = hidden or secret
-graphy = writing
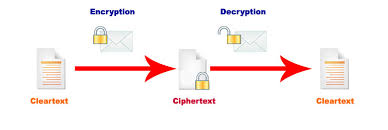
Why do we need secret communications?
How do we ensure our communications on the internet are kept ‘private’?
Your mission
Decrypt the following message:
ZNLQNL! ZNLQNL! ZNLQNL!
Demonstration: How do we share a secret key in public (10 minutes)
This is known as the key-exchange problem.
First we will see how ‘secret’ communications can happen in public. Meet Bob and Alice. Bob and Alice wish to share some information. Eve, is a snooper and is eavesdropping on all their communications.
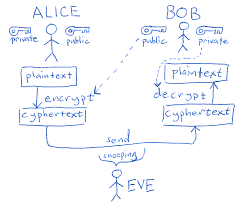
Can you work out how Alice can send the box and all it’s contents so Bob can open it, but Eve cannot?
What’s in the box? (10 minutes)
- A cipher disk for everyone
- A sealed envelope (do not open it yet) with a wax seal.
- A seemingly random pattern
Take a very close look at the seal on the envelope.
Open the envelope and see if you can piece together the clues to solve the original cipher-text:
ZNLQNL! ZNLQNL! ZNLQNL!
What are the random noise images?
Open the envelop and you find another image that appears to be noise, printed on transparency film.
Overlay this image (Image B) with the other image (Image A) printed on paper, and a hidden third image should appear.
The image pair are a form of visual encryption. One image is a kind of ‘key’ for the other.
Clue: The secret image hints at the setting for your Caesar Cipher disk.
Simple alphabetic shifting or offsetting by a number of letter places is known as the Caesar Cipher. It is also known as the Substitution Cipher or Shift Cipher. It has lots of names.
If the Cipher disk is confusing to count and read: instead of thinking of the Shift Cipher as a circle, like it appears on our disk of two alphabets, think of it as a small table, like so:
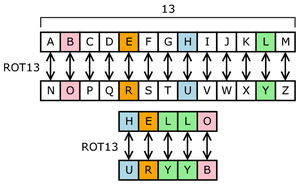
Draw one for yourself and de-encrypt the original message by looking up the encoded letters on the top row. Write down the corresponding letters on the bottom row.
The shift of 13 is special and creates a very weak cipher called ROT13.
Plenary: Discuss the following questions (2-10 minutes, as time allows)
Describe how you solved the problem?
Was it easy or hard? Too easy? Too hard?
Does the combination of securities make the cipher-text any stronger?
Why is the original encrypted message - the cypher text ZNLQNL! ZNLQNL! ZNLQNL! - weak?
How can we make cipher algorithms stronger?
What is ‘frequency analysis’. It’s a kind of cryptanalysis and can be used to attack encryption ciphers.
What uses can you think of for such visual cryptography?
What is a digital signature?
How do the ‘visual cryptography’ images work? (3 minutes)
| Original Image | Encoded Image A | Encoded Image B |
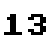 |
 |
 |
How are these images made?
One bitmap (black and white) image is processed into two complementary images - Encoded Image A and Image B.
Look closely, or zoom in , and you should see the pixel squares of the low-resolution (100x100 pixels) image.
Every pixel in the original image (50x50) is checked and replaced by a four pixel pattern selected at random from a set of six patterns (doubling the size of the original image). If a pixel contains value, i.e. is black, you can think of it as a ‘1’, if is white think of it as a ‘0’. In the second - encoded image B - the four pixel pattern is flipped when a black pixel is found.
The code to do this, below, isn’t that complicated once you get your brain around it.
Therefore, there is a very subtle difference between image A and image B. When a flipped pattern is aligned with it’s pair (using transparent film as in our example), the pixel combination make that 4x4 pixel group appear darker, replicating the tonal values of the original image.
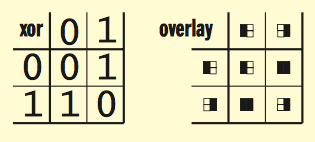
The image above represents the boolean logic of an exclusive-or operation (an XOR) and an image overlay similar to the patterns in the code sample, below.
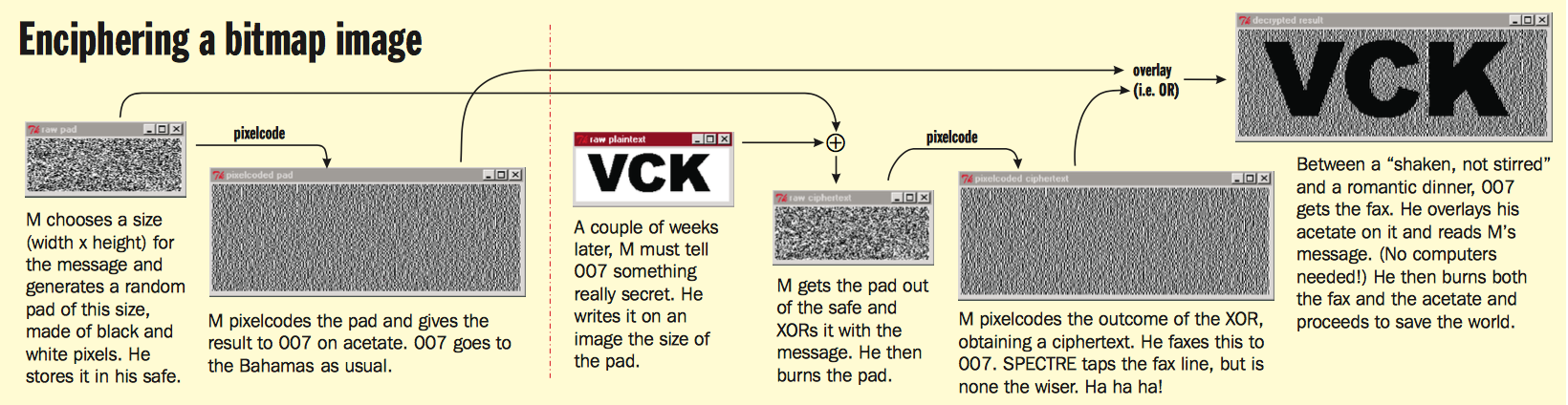
The image ‘Enciphering a bitmap image’ (above) contains an alternative description of a very similar process.
Summary
We’ve experienced secure key exchange, seen several kind of ‘keys’ and types of encryption/decryption. The Caesar cipher, especially set to 13, is famously weak and insecure. It is easily attacked and solved using ‘frequency analysis’ or ‘brute force’. For example, the common letters of the alphabet repeat more than than the rare one and looking for frequent repetition can hint at ‘A’s’ or ‘E’s’ and reveal the shift. Or ‘brute force’: try all the 25 other possibilities. That’s why our original secret had three repetitions of word and six repetitions of the common letter ‘A’ - to emphasise how patterns form in encrypted cipher-text and how this can be a weakness.
So, what are the keys in real-world cryptography?
They are often a pair of numbers, mathematically related. Remember the ‘public’ and ‘private’ keys mentioned above. These days, the keys are large numbers (several hundred digits long). Not like our two digit key ‘13’ for the Caesar Cipher. The key numbers are used as parts of mathematical problems that take a long time to solve (even with super-computers) if all parts of the original formula are missing. A Long time = years to tens of years for a very fast computer (or set of computers).
Further Explorations - Visual cryptography python code
Here is the python script that produces two images. Separately they are more or less random noise. Together - totally aligned - they reveal the source image.
See if you can follow the code - it is well commented.
Spot where the randomising of the patterns happens.
Spot the loop in a loop that steps through the X and Y pixel dimensions of the bit-map image. The code block in-the-loop in-the-loop repeats for every pixel in the images. This is called a ‘per-pixel operation’.
Find the condition in the for loop.
See if you can spot the part where the X and Y pixel coordinates of the 4x4 pixel grid are walked through and assigned a value of 1 or 0 (black or white).
If we have time we can talk through it. If not read the comments, they explain the process.
#Code source: https://github.com/LessonStudio/VisualCryptography/blob/master/visual_cryptography.py
#To run at command line type:
#
#python /path/to/script/scriptName.py path/to/source/bitmap/image.png
#
#This file takes one argument which is a file that you
#would like to split into two encrypted images.
#The original image can only be viewed by overlaying
#the two encrypted images.
#If printed on clear plastic, It can be very finicky to align
#the two images if the pixel count is too high.
#For best results keep the original image below 200x200 pixels
#and print as large as possible onto clear plastic to
#obtain the best results.
#You can go to higher resolutions but you then really have
#to be precise when aligning the two images.
#The resulting images will be twice as wide and twice as
#tall pixelwise and there is only 1 bit colour.
#we will need to read and write(create) an image
#so import libraries from the python image library
from PIL import Image, ImageDraw
import os, sys
from random import SystemRandom
random = SystemRandom()
#If you want to use the more powerful PyCrypto
#(pip install pycrypto) then uncomment the next line
#and comment out the previous two lines
#from Crypto.Random import random
#Check if the script has the correct number of command line arguments.
#Scripts run on the command line python have 'arguments'. The first (in this case)
#is the script name itself, the second is the path to the source image. Hence: '2' below
if len(sys.argv)!=2:
print "This takes one argument; the image to be split."
exit()
infile=str(sys.argv[1])
if not os.path.isfile(infile):
print "That file does not exist."
exit()
#If the file exists 'open' it by assigning its bits to a variable
img = Image.open(infile)
f, e = os.path.splitext(infile)
out_filename_A=f+"_A.png"
out_filename_B=f+"_B.png"
img=img.convert('1')#convert image to 1 bit
#Prepare two empty images for drawing - twice the size
width=img.size[0]*2
height=img.size[1]*2
out_image_A = Image.new('1', (width, height))
out_image_B = Image.new('1', (width, height))
draw_A = ImageDraw.Draw(out_image_A)
draw_B = ImageDraw.Draw(out_image_B)
#There are 6 possible patterns. The four digits represent
#4x4 pixel blocks
#These relate to the xor and overlay diagrams above
#For every black or white pixel in the original image
#the loop below replaces them systematically with
#a pattern.
#Black pixels get replaced with pattern and 'anti-pattern'
#to create a mixed black pixel on the final overlaid image
patterns=((1,1,0,0), (1,0,1,0), (1,0,0,1), (0,1,1,0), (0,1,0,1), (0,0,1,1))
#Cycle through pixels
for x in xrange(0, width/2):
for y in xrange(0, height/2):
pixel=img.getpixel((x,y))
pat=random.choice(patterns)
#A will always get the pattern
draw_A.point((x*2, y*2), pat[0]) # pat[0] is the first digit in one of the sets above
draw_A.point((x*2+1, y*2), pat[1]) # pat[1] is the second digit in one of the sets above
draw_A.point((x*2, y*2+1), pat[2]) # pat[2] is the third digit in one of the sets above
draw_A.point((x*2+1, y*2+1), pat[3]) # pat[4] is the fourth digit in one of the sets above
if pixel==0:#Dark pixel so B gets the anti pattern
draw_B.point((x*2, y*2), 1-pat[0]) #The minus here effectively 'inverts' the pattern
draw_B.point((x*2+1, y*2), 1-pat[1])
draw_B.point((x*2, y*2+1), 1-pat[2])
draw_B.point((x*2+1, y*2+1), 1-pat[3])
else:
draw_B.point((x*2, y*2), pat[0])
draw_B.point((x*2+1, y*2), pat[1])
draw_B.point((x*2, y*2+1), pat[2])
draw_B.point((x*2+1, y*2+1), pat[3])
out_image_A.save(out_filename_A, 'PNG')
out_image_B.save(out_filename_B, 'PNG')
print "Done."
What’s next
Alone or with help, see if you can get the python code working.
Discuss and discover: How do we use mathematics to make stronger encryption?
Is the maths really complicated? Or a combination of things we already know, expressed in a different way?
See:
- integer factorisation
- prime numbers
- modular (or clock) arithmetic;
- randomness.
List some of the names of other encryption methods, other than the Caesar cipher we have met?
As a start check out: RSA, the Diffie-Hellman key exchange; WEP, WEP2, for example. The descriptions get maths heavy quite quickly. Try to scan through the complicated stuff!